[백준] 11404 플로이드 (C++)

링크: https://www.acmicpc.net/problem/11404

문제

n(2 ≤ n ≤ 100)개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 m(1 ≤ m ≤ 100,000)개의 버스가 있다. 각 버스는 한 번 사용할 때 필요한 비용이 있다.

모든 도시의 쌍 (A, B)에 대해서 도시 A에서 B로 가는데 필요한 비용의 최솟값을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다.

시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있다.

출력

n개의 줄을 출력해야 한다. i번째 줄에 출력하는 j번째 숫자는 도시 i에서 j로 가는데 필요한 최소 비용이다. 만약, i에서 j로 갈 수 없는 경우에는 그 자리에 0을 출력한다.

---

풀이

단방향 그래프가 주어지고 모든 정점과 정점간의 최소 비용을 구해야 하는 문제이다.

이 문제는 '플로이드-워셜 알고리즘'으로 쉽게 풀 수 있는데, 이는 다음과 같다.

 

1. 임의의 정점 middle과 start, end가 있을 때

2. cost[start][end]와 cost[start][middle] + cost[middle][end]를 비교하여

   (start와 end 사이의 비용, start와 middle 사이의 비용 + middle과 end 사이의 비용)

3. middle을 거쳐 가는 것의 비용이 더 적은 경우 그 값을 업데이트한다.

 

위 과정을 모든 정점에 대해 진행하면 되는데, 몇 가지 주의할 사항이 있다.

 

1. 버스가 없는 경로의 비용은 무한대로 설정한다.

2. 1번 도시에서 1번도시, 2번 도시에서 2번 도시와 같이 시작 도시와 도착 도시가 같은 경우의 비용은 0으로 한다.

3. 3중 for문을 작성할 때 중간에 거쳐가는 middle을 for문의 첫 번째에 작성해야 한다.

 

3번의 경우 의아할 수 있는데, 문제에 있는 예시를 보며 그 이유를 살펴보자.

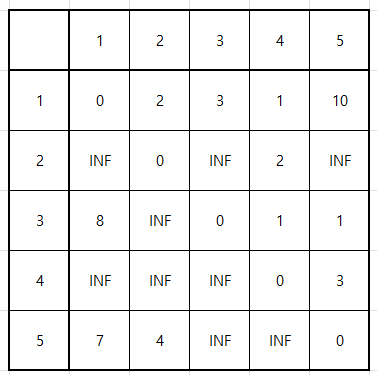
먼저 문제의 예제를  표로 정리하면 다음과 같다. 이 때 for문을 다음과 같이 작성한 후 결과를 출력하면 다음과 같다.

    for (int start = 1; start <= n; start++){
        for (int middle = 1; middle <= n; middle++){
            for (int end = 1; end <= n; end++){
                if (cost[start][end] > cost[start][middle] + cost[middle][end]){
                    cost[start][end] = cost[start][middle] + cost[middle][end];
                }
            }
        }
    }

2번 도시에서 3번 도시로 갈 때와 4번 도시에서 3번 도시로 갈 때의 값이 무한대로 나왔다.

하지만 실제로는 2 → 4 → 5 → 1 → 3 순서에 따라 2번 도시에서 3번 도시로 이동할 수 있고

4 → 5 → 1 → 3 순서에 따라 4번 도시에서 3번 도시로 이동할 수 있다.

 

위 값들이 무한대로 나온 이유는 5번 도시에서 3번 도시로 가는 경로가 아직 최적화되지 않았기 때문이다.

중간에 거쳐가는 middle을 for문 첫 번째에 두어 처음부터 빠지는 경우 없이 경로를 최적화하며 최소 비용을 구해야

모든 정점과 정점 사이의 최소 경로를 구할 수 있다.

 

코드

#include <iostream>
#include <algorithm>
// 도시의 개수는 최대 100, 비용은 최대 100,000
#define INF 10000001
using namespace std;

int cost[101][101];

void init(int n){
    // 모든 정점을 무한대로 초기화
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= n; j++){
            cost[i][j] = INF;
        }
        // 단, 시작과 도착이 같은 경우는 0으로 초기화
        cost[i][i] = 0;
    }
}

int main(){
    int n, m;
    cin >> n >> m;
    
    init(n);

    for (int i = 0; i < m; i++){
        int a, b, c;
        cin >> a >> b >> c;

        // 시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있음
        cost[a][b] = min(cost[a][b], c);
    }

    for (int middle = 1; middle <= n; middle++){
        for (int start = 1; start <= n; start++){
            for (int end = 1; end <= n; end++){
                if (cost[start][end] > cost[start][middle] + cost[middle][end]){
                    cost[start][end] = cost[start][middle] + cost[middle][end];
                }
            }
        }
    }

    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= n; j++){
            if (cost[i][j] == INF){
                cout << 0 << " ";
            }
            else{
                cout << cost[i][j] << " ";
            }
        }
        cout << endl;
    }
}