사고쳤어요
[백준] 2213 트리의 독립집합 (C++) 본문
링크: https://www.acmicpc.net/problem/2213
문제
그래프 G(V, E)에서 정점의 부분 집합 S에 속한 모든 정점쌍이 서로 인접하지 않으면 (정점쌍을 잇는 간선이 없으면) S를 독립 집합(independent set)이라고 한다. 독립 집합의 크기는 정점에 가중치가 주어져 있지 않을 경우는 독립 집합에 속한 정점의 수를 말하고, 정점에 가중치가 주어져 있으면 독립 집합에 속한 정점의 가중치의 합으로 정의한다. 독립 집합이 공집합일 때 그 크기는 0이라고 하자. 크기가 최대인 독립 집합을 최대 독립 집합이라고 한다.
문제는 일반적인 그래프가 아니라 트리(연결되어 있고 사이클이 없는 그래프)와 각 정점의 가중치가 양의 정수로 주어져 있을 때, 최대 독립 집합을 구하는 것이다.
입력
첫째 줄에 트리의 정점의 수 n이 주어진다. n은 10,000이하인 양의 정수이다. 1부터 n사이의 정수가 트리의 정점이라고 가정한다. 둘째 줄에는 n개의 정수 w1, w2, ..., wn이 주어지는데, wi는 정점 i의 가중치이다(1 ≤ i ≤ n). 셋째 줄부터 마지막 줄까지는 간선의 리스트가 주어지는데, 한 줄에 하나의 간선을 나타낸다. 간선은 정점의 쌍으로 주어진다. 입력되는 정수들 사이에는 빈 칸이 하나 있다. 가중치들의 값은 10,000을 넘지 않는 자연수이다.
출력
첫째 줄에 최대 독립집합의 크기를 출력한다. 둘째 줄에는 최대 독립집합에 속하는 정점을 오름차순으로 출력한다. 최대 독립 집합이 하나 이상일 경우에는 하나만 출력하면 된다.
풀이
"브루트 포스로 모든 경우의 수를 조사해야 하지 않나?" 라는 생각이 드는 문제이다.
한 노드의 선택 유무에 따라 다음 노드의 선택 유무가 갈리고, 노드마다 가중치가 다르기 때문이다.
하지만 그렇게 풀이를 진행하면 시간초과가 발생하고, 조금 더 체계적으로 DP를 통해 문제를 풀어나가야 한다.
예제 입력 1을 보며 풀이 과정을 살펴보자.
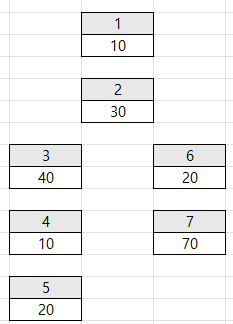
먼저 예제 1을 트리 형태로 나타내면 다음과 같다.
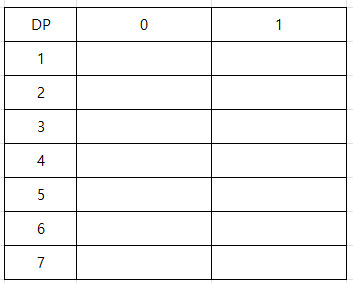
이후 DP 테이블을 채워나가야 하는데 세로에는 노드 번호, 가로에는 노드 포함 여부를 나타내며 각 값은 최대 독립집합의 크기이다.
예를 들어 dp[1][0]은 1번 노드를 포함하지 않았을 때 최대 독립집합의 크기, dp[1][1]은 1번 노드를 포함할 때 최대 독립집합의 크기이다.
그리고 자식 노드에서 부모 노드로 방문을 하지 않는 것에 유의하며 dp 테이블을 채워나가면 다음과 같을 것이다.
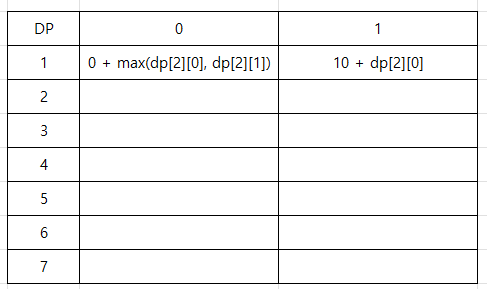
먼저 1번 노드이다.
dp[1][0]은 1번 노드를 포함하지 않았으므로 크기가 0일 것이고, 2번 노드를 포함할 수도 있고 포함하지 않을 수도 있다.
따라서 dp[1][0] = 0 + max(dp[2][0], dp[2][1]) 으로 나타낼 수 있다.
반면 dp[1][1]은 1번 노드를 포함하였으므로 크기가 10일 것이고, 2번노드를 포함할 수 없다.
따라서 dp[1][1] = 10 + dp[2][0] 으로 나타낼 수 있다.
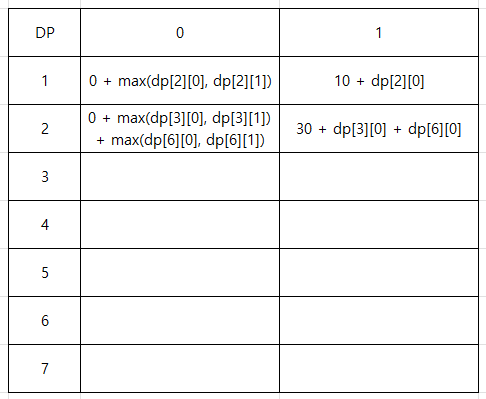
다음으로 2번 노드이다.
2번 노드는 자식 노드가 3, 6번 2개이기 때문에 2번 노드를 선택하지 않았을 때 자식 노드들을 모두 고려하여야 한다.
그 외에는 1번 노드와 마찬가지로 테이블을 채워나가면 된다.

모든 표를 채워나간 모습은 다음과 같다.
그런데 5번 노드와 7번 노드는 리프 노드이기 때문에 단순히 0 / 20, 0 / 70으로 나타낼 수 있다.
그리고 이제 거꾸로, 5번과 7번 노드부터 부모 방향으로 거꾸로 올라가며 max()를 채워나가면 된다.

최종적으로 채워진 dp 테이블이다.
정답은 dp[1][0]과 dp[1][1] 중 더 큰 값이며, 정점을 찾기 위해서는 다시 1번 노드부터 dp테이블을 찾아가면 된다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int nodes[10001];
vector<int> tree[10001];
int dp[10001][2];
bool visited[10001];
vector<int> answer;
void resetVisited(int n){
for (int i = 1; i <= n; i++){
visited[i] = false;
}
}
void dfs(int cur){
// dp[1][0]은 1번 노드가 포함되지 않았을 때 최댓값
// dp[1][1]은 1번 노드가 포함되었을 때 최댓값
dp[cur][0] = 0;
dp[cur][1] = nodes[cur];
visited[cur] = true;
for (int i = 0; i < tree[cur].size(); i++){
int next = tree[cur][i];
if (!visited[next]){
dfs(next);
dp[cur][0] += max(dp[next][0], dp[next][1]);
dp[cur][1] += dp[next][0];
}
}
}
void trace(int cur, int prev){
if (dp[cur][1] > dp[cur][0] && !visited[prev]){
answer.push_back(cur);
visited[cur] = true;
}
for (int i = 0; i < tree[cur].size(); i++){
int next = tree[cur][i];
if (next != prev){
trace(next, cur);
}
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int n;
cin >> n;
for (int i = 1; i <= n; i++){
cin >> nodes[i];
}
for (int i = 1; i < n; i++){
int a, b;
cin >> a >> b;
tree[a].push_back(b);
tree[b].push_back(a);
}
dfs(1);
resetVisited(n);
trace(1, 0);
sort(answer.begin(), answer.end());
cout << max(dp[1][0], dp[1][1]) << "\n";
for (int i = 0; i < answer.size(); i++){
cout << answer[i] << " ";
}
}
'백준 > Gold' 카테고리의 다른 글
| [백준] 17140 이차원 배열과 계산 (C++) (0) | 2025.04.03 |
|---|---|
| [백준] 1327 소트게임 (C++) (0) | 2024.11.11 |
| [백준] 1826 연료 채우기 (C++) (1) | 2024.11.08 |
| [백준] 2447 별 찍기 - 10 (C++) (0) | 2024.10.28 |
| [백준] 2437 저울 (C++) (3) | 2024.10.08 |




