사고쳤어요
[2022 KAKAO WINTER INTERNSHIP] 등산코스 정하기 (C++) 본문
링크: https://school.programmers.co.kr/learn/courses/30/lessons/118669
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
풀이
문제를 보자마자 그래프, 다익스트라로 문제를 풀어야겠다는 생각이 든 문제이다.
그런데 문제를 꼼꼼히 보면 생각보다 고려해야 할 사항이 많고 시간제한이 빡빡하다.
문제의 조건을 지키며 어떻게 효율적으로 구현할 수 있을지 생각하면 풀어낼 수 있다.
먼저 문제의 조건에서는 출입구에서 출발하여 산봉우리를 방문하고 다시 원래의 출입구로 돌아와야 한다.
그리고 우리가 구해야 할 것은 intensity가 최소가 되도록, 그리고 intensity가 같다면 산봉우리 번호가 최소가 되도록 하는 산봉우리 번호와 intensity이다.
그리고 출입구에서 산봉우리까지 이동할 때의 intensity값은 같은 경로로 원래 출입구까지 돌아올 때와 동일하다.
즉 출입구에서 산봉우리까지의 최소 intensity를 구하면, 원래 출입구로 돌아오는 것은 고려할 필요가 없다.
예시 1번을 예로 들어 풀이 과정을 살펴보자.


배열 graph에 도착 지점과 intensity를 저장한다.
예를 들어 [1, 2, 3]이 있을 때 graph[1]에 (2, 3)을 저장한다.
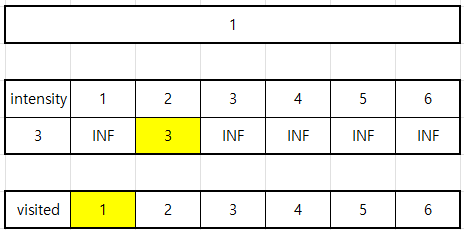
먼저 1번 gate에서 산봉우리로 이동하는 경우를 다익스트라로 구현해 보자.
1번에서 이동 가능한 다음 지점은 2번뿐이고 intensity는 3이다.

2번 gate에서 이동 가능한 경로에 대하여 intensity를 추가한다.
주의할 점으로 2번에서 4번으로 이동할 때 intensity는 2이지만 이전에 1 → 2로 이동할 때 intensity 값인 3이 더 크므로 2가 아닌 3이 저장되어야 한다.
이동 가능한 다음 경로 중 intensity가 가장 작은 곳은 4번이다.

4번 gate에서 이동 가능한 경로에 대하여 intensity를 추가한다.
마찬가지로 4번에서 6번으로 이동할 때 intensity는 1이지만 3을 저장해야 한다.
이동 가능한 다음 경로 중 intensity가 가장 작은 곳은 5, 6번이다.
여기서 5번 지역은 산봉우리임으로 현재까지 정답은 (5, 3)이 된다.
하지만 정답을 찾았다고 해서 바로 탐색을 종료해서는 안된다.
intensity가 3이면서 산봉우리 번호가 더 작은 경로가 있을 수 있기 때문이다.
만약 다음 경로를 탐색하는 중 intensity가 가장 작은 곳이 3을 넘는다면 그 때는 탐색을 종료해도 된다.
그리고 이 과정은 gate별로 모두 진행되어야 한다. 예시 1에서는 1번, 3번 출입구를 조사해보아야 한다.
위 과정을 모두 구현하여 제출하였지만, 일부 케이스에서 시간 초과가 발생하였다.
그리고 시간을 줄이기 위해 시도한 것들은 다음과 같다.
set<int> summitsSet;
bool isSummit(int spot){
if (summitsSet.find(spot) != summitsSet.end()){
return true;
}
return false;
}
문제를 구현하다보면 현재 위치한 지점이 산봉우리인지 여부를 판단해야 한다.
처음에는 단순히 summits 배열을 선형으로 탐색하며 그 여부를 확인하였다.
이를 빠른 시간 내에 판단하기 위해서는 set 자료구조를 사용해야 한다.
int djIntensity[MAX_S];
vector<int> connectedSpots;
void updateIntensity(int spot, int intensity){
for (int i = 0; i < graph[spot].size(); i++){
int nextS = graph[spot][i].first;
int nextI = graph[spot][i].second;
if (djIntensity[nextS] == MAX_I){
connectedSpots.push_back(nextS);
}
djIntensity[nextS] = min(djIntensity[nextS], max(intensity, nextI));
}
}
pair<int, int> findMinIntensity(int n, int spot){
int minIntensity = MAX_I;
int minSpot;
for (int i = 0; i < connectedSpots.size(); i++){
int nextS = connectedSpots[i];
int nextI = dijkIntensity[nextS];
if (!visited[nextS] && nextI < minIntensity){
minIntensity = nextI;
minSpot = nextS;
}
}
if (minIntensity == MAX_I){
return {-1, -1};
}
return {minSpot, minIntensity};
}
dijkIntensity[i]는 i번째 지점의 intensity를 저장하는 배열이고 connectedSpots는 이동 가능한 지점을 저장하는 벡터이다.
만약 djIntensity[i]가 INF라면 이동할 수 없었던 지점이고 connectedSpots에 새로 추가해준다.
그리고 dijkIntensity에서 최소 intensity를 찾을 때 connectedSpots에 존재하는 지점들만 찾아주면 된다.
처음에는 1~n까지를 모두 탐색하며 최소 intensity를 찾았지만 위 방법을 통해 시간을 단축시킬 수 있었다.
코드
#include <string>
#include <vector>
#include <algorithm>
#include <set>
#define MAX_S 50001
#define MAX_I 10000001
using namespace std;
set<int> summitsSet;
int answerS = 0;
int answerI = MAX_I;
vector<pair<int, int>> graph[MAX_S];
bool visited[MAX_S];
int dijkIntensity[MAX_S];
vector<int> connectedSpots;
void reset(int n){
for (int i = 1; i <= n; i++){
visited[i] = false;
dijkIntensity[i] = MAX_I;
}
connectedSpots.clear();
}
bool isSummit(int spot){
if (summitsSet.find(spot) != summitsSet.end()){
return true;
}
return false;
}
pair<int, int> findMinIntensity(int n, int spot){
int minIntensity = MAX_I;
int minSpot;
for (int i = 0; i < connectedSpots.size(); i++){
int nextS = connectedSpots[i];
int nextI = dijkIntensity[nextS];
if (!visited[nextS] && nextI < minIntensity){
minIntensity = nextI;
minSpot = nextS;
}
}
if (minIntensity == MAX_I){
return {-1, -1};
}
return {minSpot, minIntensity};
}
void updateIntensity(int spot, int intensity){
for (int i = 0; i < graph[spot].size(); i++){
int nextS = graph[spot][i].first;
int nextI = graph[spot][i].second;
if (dijkIntensity[nextS] == MAX_I){
connectedSpots.push_back(nextS);
}
dijkIntensity[nextS] = min(dijkIntensity[nextS], max(intensity, nextI));
}
}
void solve(int n, int gate){
while (true){
pair<int, int> next = findMinIntensity(n, gate);
int nextSpot = next.first;
int nextIntensity = next.second;
if (nextSpot == -1 || nextIntensity > answerI){
return;
}
visited[nextSpot] = true;
if (isSummit(nextSpot)){
if (nextIntensity < answerI || (nextIntensity == answerI && nextSpot < answerS)){
answerI = nextIntensity;
answerS = nextSpot;
}
continue;
}
updateIntensity(nextSpot, nextIntensity);
}
}
vector<int> solution(int n, vector<vector<int>> paths, vector<int> gates, vector<int> summits) {
vector<int> answer;
for (int path = 0; path < paths.size(); path++){
int i = paths[path][0];
int j = paths[path][1];
int w = paths[path][2];
graph[i].push_back({j, w});
graph[j].push_back({i, w});
}
for (int i = 0; i < summits.size(); i++){
summitsSet.insert(summits[i]);
}
for (int i = 0; i < gates.size(); i++){
reset(n);
int gate = gates[i];
visited[gate] = true;
updateIntensity(gate, 0);
solve(n, gate);
}
answer.push_back(answerS);
answer.push_back(answerI);
return answer;
}
'프로그래머스' 카테고리의 다른 글
| [프로그래머스] 비밀 코드 해독 (C++) (0) | 2025.03.20 |
|---|---|
| [프로그래머스] 아이템 줍기 (C++) (1) | 2024.11.07 |
| [2024 KAKAO WINTER INTERNSHIP] 주사위 고르기 (C++) (0) | 2024.07.17 |
| [2024 KAKAO WINTER INTERNSHIP] 도넛과 막대 그래프 (C++) (0) | 2024.07.16 |
| [2024 KAKAO WINTER INTERNSHIP] 가장 많이 받은 선물 (C++) (2) | 2024.07.16 |



