사고쳤어요
[백준] 2637 장난감 조립 (C++) 본문
링크: https://www.acmicpc.net/problem/2637
2637번: 장난감 조립
첫째 줄에는 자연수 N(3 ≤ N ≤ 100)이 주어지는데, 1부터 N-1까지는 기본 부품이나 중간 부품의 번호를 나타내고, N은 완제품의 번호를 나타낸다. 그리고 그 다음 줄에는 자연수 M(3 ≤ M ≤ 100)이 주
www.acmicpc.net
문제
우리는 어떤 장난감을 여러 가지 부품으로 조립하여 만들려고 한다. 이 장난감을 만드는데는 기본 부품과 그 기본 부품으로 조립하여 만든 중간 부품이 사용된다. 기본 부품은 다른 부품을 사용하여 조립될 수 없는 부품이다. 중간 부품은 또 다른 중간 부품이나 기본 부품을 이용하여 만들어지는 부품이다.
예를 들어보자. 기본 부품으로서 1, 2, 3, 4가 있다. 중간 부품 5는 2개의 기본 부품 1과 2개의 기본 부품 2로 만들어진다. 그리고 중간 부품 6은 2개의 중간 부품 5, 3개의 기본 부품 3과 4개의 기본 부품 4로 만들어진다. 마지막으로 장난감 완제품 7은 2개의 중간 부품 5, 3개의 중간 부품 6과 5개의 기본 부품 4로 만들어진다. 이런 경우에 장난감 완제품 7을 만드는데 필요한 기본 부품의 개수는 1번 16개, 2번 16개, 3번 9개, 4번 17개이다.
이와 같이 어떤 장난감 완제품과 그에 필요한 부품들 사이의 관계가 주어져 있을 때 하나의 장난감 완제품을 조립하기 위하여 필요한 기본 부품의 종류별 개수를 계산하는 프로그램을 작성하시오.
입력
첫째 줄에는 자연수 N(3 ≤ N ≤ 100)이 주어지는데, 1부터 N-1까지는 기본 부품이나 중간 부품의 번호를 나타내고, N은 완제품의 번호를 나타낸다. 그리고 그 다음 줄에는 자연수 M(3 ≤ M ≤ 100)이 주어지고, 그 다음 M개의 줄에는 어떤 부품을 완성하는데 필요한 부품들 간의 관계가 3개의 자연수 X, Y, K로 주어진다. 이 뜻은 "중간 부품이나 완제품 X를 만드는데 중간 부품 혹은 기본 부품 Y가 K개 필요하다"는 뜻이다. 두 중간 부품이 서로를 필요로 하는 경우가 없다.
출력
하나의 완제품을 조립하는데 필요한 기본 부품의 수를 한 줄에 하나씩 출력하되(중간 부품은 출력하지 않음), 반드시 기본 부품의 번호가 작은 것부터 큰 순서가 되도록 한다. 각 줄에는 기본 부품의 번호와 소요 개수를 출력한다.
정답은 2,147,483,647 이하이다.
풀이
문제를 처음 본 순간, DFS를 사용하면 문제가 쉽게 풀릴 것이라 생각하였다.
선택된 부품이 중간 부품이라면 재귀를 통해 해당 부품의 다른 재료 부품들을 호출하고,
선택된 부품이 기본 부품이라면 개수만큼 추가해주었다.
void solve(int target, int amount){
// 장난감이 기본 부품인 경우
if (!toys[target].size()){
answer[target] += amount;
return;
}
// 장난감이 중간 부품인 경우
else{
for (int i = 0; i < toys[target].size(); i++){
solve(toys[target][i].first, toys[target][i].second * amount);
}
}
}
하지만 시간이 초과되었고, 더 나은 방법을 찾아보았다.

두 번째로 생각한 방법은 큐에 재료 부품과 그 수를 저장하는 방식이었다.
void solve(){
queue<pair<int, int>> q;
q.push({n, 1});
while (!q.empty()){
int target = q.front().first;
int amount = q.front().second;
q.pop();
// 장난감이 기본 부품인 경우
if (!toys[target].size()){
answer[target] += amount;
}
// 장난감이 중간 부품인 경우
else{
for (int i = 0; i < toys[target].size(); i++){
q.push({toys[target][i].first, amount*toys[target][i].second});
}
}
}
}
하지만 위 방식 역시 메모리 초과가 발생하였고, 시간과 메모리를 절약할 수 있는 다른 방법이 필요하였다.

위의 방법들이 비효율적이었던 이유는 같은 번호의 부품들이 여러 번 계산되기 때문이다.
예를 들어 예제 입력 1에서는 5번 부품의 계산을 처리한 뒤 6번 부품의 계산을 처리한다면 5번이 다시 추가되고
5번 부품을 두 번 계산하게 된다.
반면 6번 부품의 계산을 처리하고 5번 부품의 계산을 처리한다면 5번 부품을 한 번만 계산하면 된다.
이에, 위상정렬을 활용하여 우선순위를 정해두고 그 순서대로 계산을 한다면 같은 부품을 여러 번 계산할 필요 없이
효율적으로 필요한 부품의 개수를 구할 수 있다!
우선순위는 '부품이 다른 부품의 재료로 쓰인 횟수'를 저장하여 사용하였다.
예제 입력 1을 그림으로 그려보면 다음과 같다.
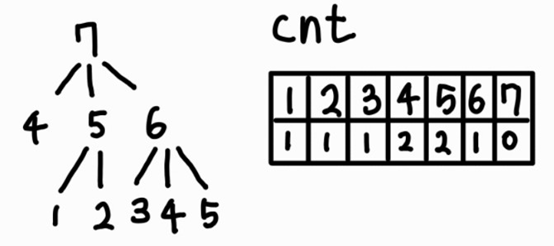
우선 순위는 배열 cnt에 저장해두었고, 각 부품이 다른 부품의 재료로 쓰인 횟수를 저장하였다.
여기서 cnt 값이 0인 7번 부품을 먼저 계산한다.
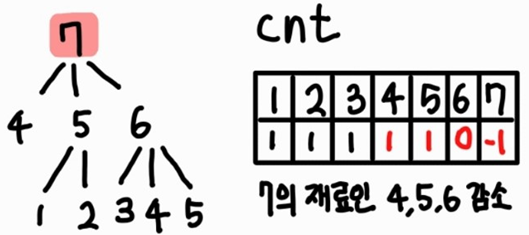
7번 부품을 계산함에 따라 7번의 재료 부품인 4, 5, 6번 부품들의 cnt 값이 1씩 감소된다.
이어서 cnt 값이 0인 6번 부품을 계산한다.
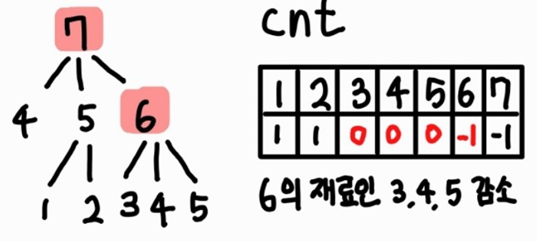
6번 부품을 계산함에 따라 6번의 재료 부품인 3, 4, 5번 부품들의 cnt 값이 1씩 감소된다.
이어서 cnt 값이 0인 3번 부품을 계산한다.

3번 부품은 기본 부품이므로 다른 부품들의 cnt 값은 감소하지 않는다.
이어서 cnt 값이 0인 부품을 계산하는 과정을 반복하면
같은 부품을 여러 번 계산할 필요 없이 효율적으로 모든 부품의 개수를 구할 수 있다.
코드
#include <iostream>
#include <vector>
using namespace std;
#define MAX 101
int n, m;
// {필요 부품, 부품 개수}로 저장
vector<pair<int, int>> toys[MAX];
// 다른 부품의 재료가 되는 횟수 저장
int cnt[MAX];
int answer[MAX];
void solve(){
while (true){
// cnt가 0인 장난감 부품을 찾음
int toy;
for (int i = 1; i <= n; i++){
if (cnt[i] == 0){
toy = i;
cnt[i]--;
break;
}
// 더 이상 장난감을 필요로 하지 않는 경우 종료
if (i == n){
return;
}
}
// target이 기본 부품인 경우
if (!toys[toy].size()){
continue;
}
// target이 중간 부품인 경우
else{
for (int i = 0; i < toys[toy].size(); i++){
int target = toys[toy][i].first;
int amount = toys[toy][i].second;
answer[target] += answer[toy]*amount;
cnt[target]--;
}
answer[toy] = 0;
}
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> n >> m;
for (int i = 0; i < m; i++){
int a, b, c;
cin >> a >> b >> c;
toys[a].push_back({b,c});
// 부품이 다른 부품의 재료가 되는 경우 count[b] 증가
cnt[b]++;
}
answer[n] = 1;
solve();
for (int i = 1; i <= n; i++){
if (answer[i]){
cout << i << " " << answer[i] << "\n";
}
}
}

'백준 > Gold' 카테고리의 다른 글
| [백준] 2616 소형기관차 (C++) (1) | 2024.03.18 |
|---|---|
| [백준] 4179 불! (C++) (1) | 2024.03.17 |
| [백준] 14891 톱니바퀴 (C++) (0) | 2024.03.17 |
| [백준] 23818 원수의 원수 (C++) (3) | 2024.03.11 |
| [백준] 1197 최소 스패닝 트리 (C++) (0) | 2024.03.07 |




